इयत्ता 10वी गणित व्यायाम 10.2 NCERT सोल्यूशन्स PDF

खालील सर्व प्रश्नांची उत्तरे तपासा:

दहावीच्या गणितासाठी NCERT सोल्यूशन्स मंडळे – व्यायाम १०.२

Q.1 ते 3 मध्ये, योग्य पर्याय निवडा आणि समर्थन द्या.

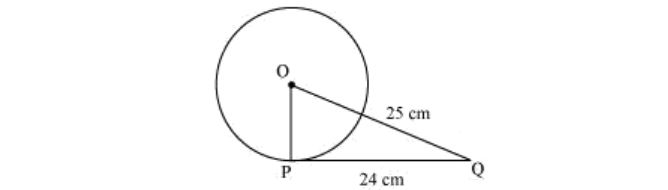
1. बिंदू Q पासून, स्पर्शिकेची वर्तुळाची लांबी 24 सेमी आहे आणि Q चे अंतर बिंदूपासून आहे. केंद्र 25 सेमी आहे. वर्तुळाची त्रिज्या आहे

(A) 7 सेमी

(ब) 12 सेमी

(C) 15 सें.मी

(D) 24.5 सेमी

उपाय:

O हे वर्तुळाचे केंद्र असू द्या.

ते पाहता,

OQ = 25 सेमी आणि PQ = 24 सेमी

OP ⊥ PQ (त्रिज्या संपर्काच्या बिंदूवरील स्पर्शिकेला लंब असते)

ΔOPQ मध्ये पायथागोरस प्रमेय लागू करणे,

ओ.पी² + PQ² = OQ²

ओ.पी² + २४² = 25²

ओ.पी² = ६२५ − ५७६

ओ.पी² = 49

ओपी = 7

म्हणून, वर्तुळाची त्रिज्या 7 सें.मी.

म्हणून, पर्यायी (A) योग्य आहे

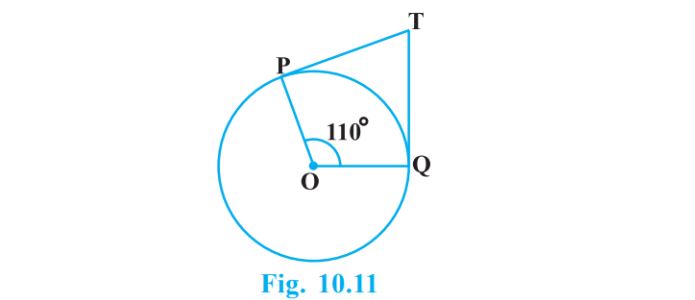
2. अंजीर 10.11 मध्ये, जर TP आणि TQ या दोन स्पर्शिका असतील तर केंद्र ओ असलेले वर्तुळ जेणेकरून∠POQ = 110°, tकोंबडी ∠PTQ समान आहे

(A) 60°

(B) 70°

(C) 80°

(D) 90°

उपाय:

हे दिले आहे की TP आणि TQ स्पर्शिका आहेत.

म्हणून, या स्पर्शिकांकडे काढलेली त्रिज्या स्पर्शिकेला लंब असेल.

अशा प्रकारे, OP ⊥ TP आणि OQ ⊥ TQ

∠OPT = 90^o

∠OQT = 90^o

चतुर्भुज POQT मध्ये,

सर्व आतील कोनांची बेरीज = 360^o

∠OPT + ∠POQ +∠OQT + ∠PTQ = 360^o

⇒ 90^o + ११०^o + ९०^o +∠PTQ = 360^o

⇒ ∠PTQ = ७०^o

म्हणून, पर्यायी (B) योग्य आहे.

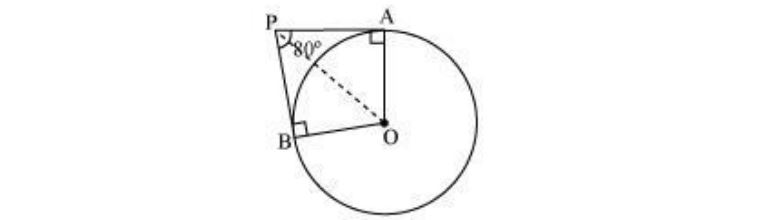
3. जर PA आणि PB बिंदू P पासून केंद्र O असलेल्या वर्तुळात एकमेकांकडे कललेले असतील तर 80° चा कोन, नंतर POA समान आहे

(A) 50°

(B) 60°

(C) 70°

(D) 80°

उपाय:

असे दिले आहे की PA आणि PB स्पर्शिका आहेत.

म्हणून, या स्पर्शिकांकडे काढलेली त्रिज्या स्पर्शिकेला लंब असेल.

अशा प्रकारे, OA ⊥ PA आणि OB ⊥ PB

∠OBP = 90^o

∠OAP = 90^o

AOBP मध्ये,

सर्व आतील कोनांची बेरीज = 360^o

∠OAP + ∠APB +∠PBO + ∠BOA = 360^o

90^o + ८०^o + ९०^o +∠BOA = 360^o

∠BOA = 100^o

ΔOPB आणि ΔOPA मध्ये,

AP = BP (बिंदूपासून स्पर्शिका)

OA = OB (वर्तुळाची त्रिज्या)

OP = OP (सामान्य बाजू)

म्हणून, ΔOPB ≅ΔOPA (SSS एकरूपता निकष)

A ↔ B, P ↔ P, O ↔ O

आणि अशा प्रकारे, ∠POB = ∠POA

∠POA = 1/2∠AOB = 100/2 = 50^o

म्हणून, पर्यायी (A) योग्य आहे.

4. वर्तुळाच्या व्यासाच्या टोकाला काढलेल्या स्पर्शिका समांतर आहेत हे सिद्ध करा.

उपाय:

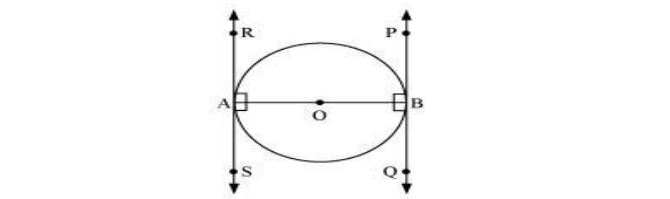
AB हा वर्तुळाचा व्यास मानू. दोन स्पर्शिका PQ आणि RS बिंदू A आणि B वर काढल्या आहेत

अनुक्रमे

अशा प्रकारे, OA ⊥ RS आणि OB ⊥ PQ

∠OAR = 90^o

∠OAS = 90^o

∠OBP = 90^o

∠OBQ = 90^o

असे निरीक्षण करता येईल

∠OAR = ∠OBQ (पर्यायी आतील कोन)

∠OAS = ∠OBP (पर्यायी आतील कोन)

पर्यायी आतील कोन समान असल्याने, रेषा PQ आणि RS समांतर असतील.

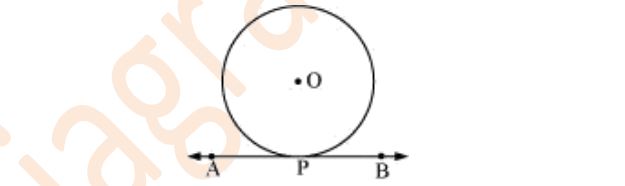
5. वर्तुळाच्या स्पर्शिकेच्या संपर्काच्या बिंदूवरील लंब मध्यभागी जातो हे सिद्ध करा.

उपाय: O केंद्र असलेल्या वर्तुळाचा विचार करू या. AB ला P वर वर्तुळाला स्पर्श करणारी स्पर्शिका असू द्या.

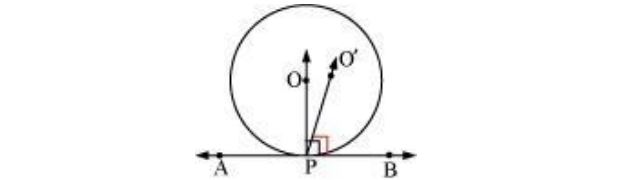
P वरील AB ला लंब O केंद्रातून जात नाही असे गृहीत धरू. त्याला पुढे जाऊ द्या

दुसरा बिंदू O’.

OP आणि O’P मध्ये सामील व्हा

P वर AB ला लंब असल्याप्रमाणे O’ मधून जातो, म्हणून,

∠O’PB = 90° ……….. (1)

मध्यभागी जोडणारी रेषा आणि वर्तुळाच्या स्पर्शिकेचा संपर्क बिंदू प्रत्येकाला लंब असतो

इतर

∴ ∠OPB = 90° ………. (२)

समीकरणे (1) आणि (2) यांची तुलना केल्यास, आम्हाला मिळते

∠O’PB = ∠OPB ………. (३)

आकृतीवरून असे लक्षात येते की,

∠O’PB < ∠OPB ……….. (४)

त्यामुळे, ∠O’PB = ∠OPB शक्य नाही. हे तेव्हाच शक्य आहे, जेव्हा O’P ही ओळ OP शी जुळते.

म्हणून, P मधून AB ला लंब O केंद्रातून जातो.

खालील लिंकवरून सर्व NCERT उपाय तपासा आणि डाउनलोड करा: