CBSE इयत्ता 10 गणित धडा 8 त्रिकोणमिती नोट्सचा परिचय, PDF डाउनलोड करा

CBSE वर्ग 10 ची त्रिकोणमिती नोट्सची ओळख: या लेखात, आपण त्रिकोणमितीच्या परिचयासाठी पुनरावृत्ती नोट्स शोधू शकता. इयत्ता 10 मधील विद्यार्थ्यांची धडा संबंधित समज सुधारण्यासाठी येथे लहान आणि हस्तलिखित नोट्स प्रदान केल्या आहेत.

CBSE इयत्ता 10 व धडा 8 त्रिकोणमिती नोट्सचा परिचय साठी PDF डाउनलोड करा

त्रिकोणमितीचा परिचय वर्ग 10 च्या नोट्स: चालू शैक्षणिक सत्र 2023-2024 च्या विद्यार्थ्यांसाठी इयत्ता 10वीच्या त्रिकोणमितीच्या परिचयाच्या पुनरावृत्ती नोट्स या लेखासोबत जोडल्या आहेत. त्रिकोणमितीवरील या छोट्या आणि हस्तलिखित नोट्स इयत्ता 10 मधील विद्यार्थ्यांना विषयाशी संबंधित त्यांच्या शंका दूर करण्यात आणि त्याच वेळी त्यांच्या आकलनाचे विश्लेषण करण्यास मदत करतील.

पुनरावृत्ती नोट्स परीक्षांसाठी तुमचे मार्गदर्शक आहेत. विषय आणि तपशील विद्यार्थ्यांना समजेल याची खात्री करण्यासाठी प्रकरणातील सर्व संबंधित आणि महत्त्वाचे भाग निवडले जातात आणि एकाच ठिकाणी थोडक्यात सादर केले जातात. तसेच, त्रिकोणमितीवरील NCERT सोल्यूशन्स कसे सोडवता येतात ते तपासा. व्यायामाचे प्रश्न कसे सोडवावेत याची योग्य कल्पना देण्यासाठी आवश्यक सूत्रे आणि प्रमेये छोट्या नोट्समध्ये मांडण्यात आली आहेत.

CBSE वर्ग 10 त्रिकोणमिती त्रिकोणमिती पुनरावृत्ती नोट्सचा परिचय

त्रिकोणमितीच्या परिचयावर इयत्ता 10 च्या पुनरावृत्ती नोट्स तपासा आणि त्याचसाठी PDF डाउनलोड लिंकसह. या नोट्स अद्ययावत CBSE इयत्ता 10 च्या गणिताच्या अभ्यासक्रम 2024 नुसार तयार केल्या आहेत. त्यामुळे आमच्या विषय तज्ञांनी बनवलेल्या या छोट्या नोट्सचा संदर्भ देताना विद्यार्थी निश्चिंत राहू शकतात.

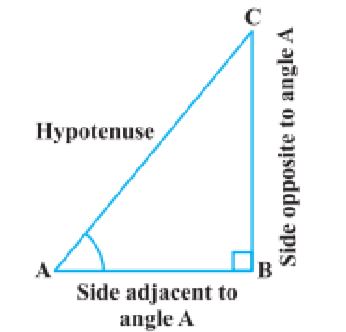
त्रिकोणमिती म्हणजे त्रिकोणाच्या बाजू आणि कोनांमधील संबंधांचा अभ्यास. ‘ट्रिगोनोमेट्री’ हा शब्द ग्रीक शब्द ‘ट्राय’ (म्हणजे तीन), ‘गोन’ (म्हणजे बाजू) आणि ‘मेट्रॉन’ (म्हणजे मोजमाप) पासून बनला आहे.
कोनाचे त्रिकोणमितीय गुणोत्तर– काटकोन त्रिकोणाच्या बाजूंच्या तीव्र कोनांच्या संदर्भात असलेल्या गुणोत्तरांना कोनाचे त्रिकोणमितीय गुणोत्तर म्हणतात.
काटकोन त्रिकोण ABC विचारात घ्या, जेथे A हा तीव्र कोन आहे, नंतर BC ही कोनाच्या विरुद्ध बाजू आहे आणि AB ही कोन A च्या समीप बाजू आहे. AC काटकोन B च्या विरुद्ध असल्याने, ते कर्ण आहे.

या प्रकरणात त्रिकोणमितीय गुणोत्तर असेल:

त्रिकोणमितीय गुणोत्तरांचे संक्षिप्त रूप:

साइन ए- सिन ए

कोसाइन A- cos A

स्पर्शिका A- tan A

Cosecant A- cosec A (sin A च्या समोर)

Secant A- sec A (cos A च्या विरुद्ध)

Cotangent A- cot A (tan A च्या समोर)

कोन समान राहिल्यास कोनाच्या त्रिकोणमितीय गुणोत्तरांची मूल्ये त्रिकोणाच्या बाजूंच्या लांबीनुसार बदलत नाहीत.
पायथागोरस प्रमेय– (उंची)²= (लांबी)² – (रुंदी)²
एक गुणोत्तर दिले असल्यास इतर त्रिकोणमितीय गुणोत्तर कसे शोधायचे?