इयत्ता 9, 10, 11 आणि 12 वी साठी संपूर्ण फॉर्म्युला यादी

त्रिकोणमिती सूत्रे: गणितात त्रिकोणमिती आणि कॅल्क्युलसपेक्षा विद्यार्थ्यांना जास्त त्रास देणारे फार थोडे विषय आहेत. खरं तर, हा अनेक प्रगत गणित संकल्पनांचा आधार आहे आणि भौतिकशास्त्रासारख्या इतर विषयांमध्ये देखील त्याचा वापर केला जातो. त्यामुळे, विद्यार्थ्यांनी त्रिकोणमिती मनापासून शिकणे महत्त्वाचे आहे. अशी शेकडो सूत्रे आणि ओळखी आहेत जी विद्यार्थ्यांना त्यांच्या शाळेच्या काळात लक्षात ठेवावी लागतात.

त्रिकोणमिती आणि त्यानंतर कॅल्क्युलस ही विद्यार्थ्यांसाठी डोकेदुखी आहे परंतु परीक्षा उत्तीर्ण होण्यासाठी आणि गणिताचे उच्च शिक्षण घेण्यासाठी आवश्यक आहे. त्रिकोणमितीमध्ये अनेक वास्तविक-जागतिक अनुप्रयोग देखील आहेत.

नावाप्रमाणेच, त्रिकोणमिती ही गणिताची शाखा आहे जी काटकोन त्रिकोणाच्या बाजू आणि कोनांमधील संबंधांचा अभ्यास करते. हे खगोलशास्त्र, कार्टोग्राफी, भूगोल, नौदल आणि विमानचालन उद्योगांमध्ये वापरले जाते. आम्ही तुमच्यासाठी खालील त्रिकोणमिती सूत्र pdf घेऊन आलो आहोत.

त्रिकोणमिती सूत्र PDF

वर्ग 10 साठी त्रिकोणमितीची मूलभूत तत्त्वे

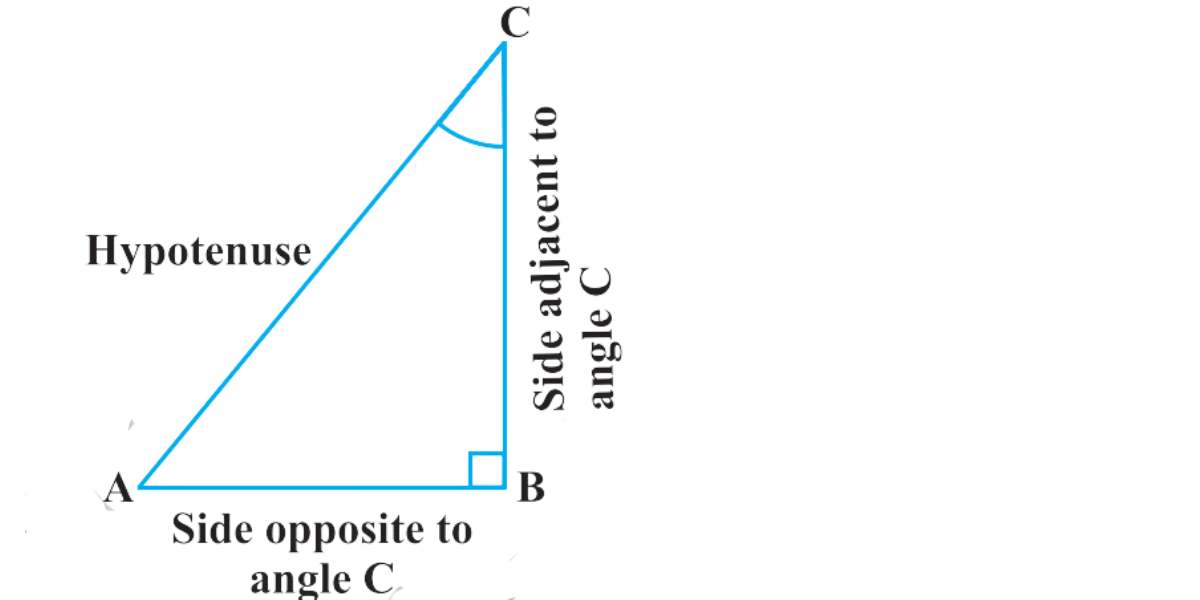
वर दिलेल्या काटकोन त्रिकोण ABC मधील A चे त्रिकोणमितीय गुणोत्तर खालीलप्रमाणे परिभाषित केले आहेत:

• ∠ A चे साइन = कोन A/hypotenuse = BC/AC च्या विरुद्ध बाजू
• कोसाइन ∠ A = कोनाला लागून असलेली बाजू A/hypotenuse = AB/AC
• ∠ A ची स्पर्शिका = कोन A च्या विरुद्ध बाजू/कोनाला लागून असलेली बाजू A = BC/AB
• ∠ A = 1/ ∠A = AC/BC चा कोसेकंट
• ∠A = 1/∠A = AC/AB चा कोसाइन
• ∠ A = 1/ ∠A = AB/BC ची स्पर्शिका

त्रिकोणमिती सारणी

त्रिकोणमितीय सह-कार्य ओळख

• sin (π/2 – A) = cos A & cos (π/2 – A) = sin A
• sin (π/2 + A) = cos A & cos (π/2 + A) = – sin A
• sin (3π/2 – A) = – cos A & cos (3π/2 – A) = – sin A
• sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A
• sin (π – A) = sin A & cos (π – A) = – cos A
• sin (π + A) = – sin A & cos (π + A) = – cos A
• sin (2π – A) = – sin A & cos (2π – A) = cos A
• sin (2π + A) = sin A & cos (2π + A) = cos A

पदवी मध्ये सह-कार्य ओळख

• sin(90°−x) = cos x
• cos(90°−x) = sin x
• tan(90°−x) = cot x
• cot(90°−x) = टॅन x
• sec(90°−x) = cosec x
• cosec(90°−x) = सेकंद x

वर्ग 12 साठी त्रिकोणमिती सूत्रे

व्यस्त त्रिकोणमितीय कार्ये

वाचा: CBSE इयत्ता 12 गणित धडा 2 व्यस्त त्रिकोणमितीय कार्ये सूत्रांची यादी, महत्त्वाच्या व्याख्या आणि उदाहरणे

• पाप^-1x = – पाप^-1x
• कारण^-1x = π – cos^-1x
• टॅन^-1(-x) = -tan^-1x
• cosec⁻¹(-x) = -cosec⁻¹x
• सेकंद^-1(-x) = π – से^-1x
• खाट^-1(-x) = π – खाट^-1x
• पाप^-1x + cos^-1x = π/2
• टॅन^-1x + खाट^-1x = π/2
• सेकंद^-1x + cosec^-1x = π/2
• पाप^-1x = – पाप^-1x
• कारण^-1x = π – cos^-1x
• टॅन^-1(-x) = -tan^-1x
• cosec⁻¹(-x) = -cosec⁻¹x
• सेकंद^-1(-x) = π – से^-1x
• खाट^-1(-x) = π – खाट^-1x
• पाप^-1x + cos^-1x = π/2
• टॅन^-1x + खाट^-1x = π/2
• सेकंद^-1x + cosec^-1x = π/2

व्यस्त त्रिकोणमितीय कार्यांचे दुहेरी

• २ टॅन^-1x = पाप^-1(2x/1+ x²)
• = cos^-1(1-x²/1+x²)
• = टॅन^-1(2x/1-x²)
• 2 पाप^-1x = पाप^-1(2x.√(1 – x²))
• 2cos^-1x = cos^-1(2x²– १)

व्यस्त त्रिकोणमितीय कार्यांचे तिप्पट

• 3 पाप^-1x = पाप^-1(3x – 4x³)
• 3cos^-1x = cos^-1(4x³– 3x)
• 3tan^-1x = टॅन^-1(3x – x³/1 – 3x²)